Im Internet kursiert ein einziges Foto von Georg Pick. Es zeigt einen jungen Mann mit kurzem Haar und einem Anflug von Schnurrbart. Dazu, wie damals die Mode, eine mächtige Krawatte und ein verwegener Blick.

Pick war etwas jünger als Sigmund Freud, etwas älter als Arthur Schnitzler. Er wurde in Wien-Leopoldstadt geboren und studierte an der Universität Wien Mathematik – offenbar mit Erfolg, denn bald trat er eine Stelle an der ehrwürdigen Prager Universität an, wo er es zum Professor und Dekan brachte. Sein Kollege war kein Geringerer als der berühmte Ernst Mach. Ein Jahr lang, um 1910, gehörte auch Einstein zu Picks Fakultät.

Nach einer schönen Laufbahn emeritierte Georg Pick im Jahr 1929 und kehrte in seine Heimatstadt zurück. Keine zehn Jahre später musste er sich über die Grenze nach Prag retten. Auch dort holte ihn Hitler ein. Der achtzigjährige Pick wurde deportiert und 1942 in Theresienstadt umgebracht. Von Leopoldstadt nach Theresienstadt – eine solche Lebensreise war kein Einzelschicksal.

Dokumente über Picks Leben sind rar. Aber er hat seine Spuren in der Mathematik hinterlassen, durch anspruchsvolle Beiträge auf vielen Gebieten, besonders der komplexen Analysis. Seine bekannteste Entdeckung jedoch ist ein Lehrsatz, der überhaupt keine mathematische Vorbildung erfordert und selbst Zwölfjährigen Spaß machen kann – Beweis inbegriffen!

Wie groß ist ein Vieleck

Schon in der Volksschule lernt man, was ein Vieleck ist. Auf einem Blatt Papier setzt man den Stift an, zieht eine geradlinige Strecke, dann ohne abzusetzen die nächste, dann die nächste und so weiter, ohne je den schon gezeichneten Streckenzug zu berühren, bis man zuletzt wieder zum Ausgangspunkt zurückkehrt. Dann ist das Vieleck fertig. Es besteht aus Eckpunkten und Strecken, die sie verbinden.

Das ergibt Dreiecke, Achtecke, Zwölfecke ... Sie können regelmäßig sein oder auch nicht, das spielt keine Rolle. Und wie groß ist das Vieleck? Kein Problem. Auch das komplizierteste Vieleck kann man in einfachere zerlegen: in Dreiecke, Rechtecke, Trapeze, für die man leicht den Flächeninhalt errechnet. Man misst Höhen und Breiten, multipliziert, halbiert da und dort und zählt zuletzt alles zusammen. Kinderspiel.

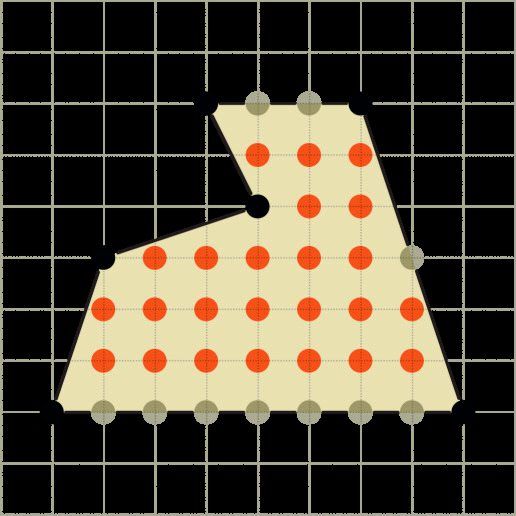
Die Vielecke von Pick zeichnet man auf kariertem Papier. Das Zeichenblatt ist also mit einem Gitter dünner Linien überzogen, und die Eckpunkte der Vielecke liegen auf dem Gitter – dort, wo sich zwei Gitterlinien schneiden. Solche Vielecke nennt man Gitterpolygone.

Und für diese Gitterpolygone hat Pick seinen Satz bewiesen, nämlich dass man den Flächeninhalt durch ein einfaches Rezept erhält. Man zähle alle Gitterpunkte am Rand (dazu gehören die Eckpunkte, aber vielleicht auch andere Gitterpunkte auf den Strecken) und dividiere diese Zahl durch 2. Dann zähle man alle Gitterpunkte im Inneren und addiere sie dazu. Dann ziehe man 1 ab. Und fertig. Man hat den Flächeninhalt gefunden, und das durch bloßes Zählen, ohne zu messen.

Erhält man etwa die Zahl 31, so heißt das: Die Fläche ist 31-mal so groß wie das Einheitsquadrat (also das kleinste Karo auf dem karierten Papier). Ganz genau 31, übrigens: nicht 31,04. Es kann nur eine ganze Zahl herauskommen oder eine ganze Zahl plus 1/2.

Während man sich beim Messen oft mit angenäherten Werten zufriedengeben muss, wird bei Pick nur gezählt: Die Gitterpunkte im Inneren zählen ganz, die am Rand halb. Ein solcher Randpunkt gehört ja gewissermaßen nur halb zum Vieleck, er ist weder ganz drinnen noch ganz draußen.

Überprüfung von Picks Rezept

Es ist einfach, Picks Rezept an ein paar Beispielen zu überprüfen. Beim Einheitskaro – einem einzigen kleinen Quadrat auf unserem karierten Papier – gibt es überhaupt keinen inneren Punkt und 4 Ecken. Diese zählen je halb, ergibt 2. Davon zieht man eins ab, ergibt Flächeninhalt 1. Passt.

Wenn man das kleine Quadrat noch weiter teilt, durch eine Diagonale, erhält man zwei Dreiecke. Ein solches Dreieck hat 3 Randpunkte, jeder zählt halb. Man zieht 1 ab und hat den Flächeninhalt: 1/2. Kleiner geht’s nimmer.

Jetzt kann man die Formel an größeren achsenparallelen Rechtecken ausprobieren. Das Ergebnis: Picks Verfahren liefert immer Länge mal Breite, wie es sein soll. Ebenso bei rechtwinkeligen achsenparallelen Dreiecken, die man ja erhält, wenn man ein Rechteck mittels Diagonale zerlegt.

Und wer einmal so weit ist, ist dem Beweis des Satzes von Pick schon auf der Spur: Denn alle Gitterpolygone lassen sich ja in Dreiecke zerlegen. Allerdings, Vorsicht! Das müssen nicht unbedingt achsenparallele rechtwinkelige Dreiecke sein. Also gehört noch eine gute Idee her. Sie sei dem geneigten Lesepublikum vorenthalten. Man verrät ja auch nicht die Auflösung im Kriminalroman.

Hat der Satz von Pick Anwendungen? Wie man’s nimmt. Es ist so ähnlich wie die Frage, ob ein guter Witz Anwendungen hat. Ein Witz kann tiefe Einsicht vermitteln und doch ohne praktischen Nutzen sein. Aber wenn schon die Frage im Raum steht: Ja, der Satz von Pick hat bemerkenswerte Anwendungen – und zwar in der Mathematik!

Hier ein Beispiel: Eine der tiefsten Erkenntnisse ist die Euler’sche Formel für Polyeder, also für Körper im Raum, die von Vielecken begrenzt sind. Der Würfel etwa ist ein Polyeder. Er hat 6 Flächen, 12 Kanten und 8 Ecken. Die Formel von Euler gilt für alle Polyeder, die konvex sind (also nicht hohlwangig oder durchlöchert).

Sie besagt: Wird die Zahl der Ecken und der Flächen addiert, so ergibt das die Zahl der Kanten plus 2. Beim Würfel stimmt die Formel: 6+8=12+2. Bei Pyramiden auch. Bei Rhomben auch und bei Parallelepipeden, bei Prismen und Ikosaedern, Dodekaedern und überhaupt immer! In der griechischen Mathematik spielten die regelmäßigen Körper eine zentrale Rolle – und doch wurde die Formel erst in der Neuzeit gefunden: Ecken + Flächen = Kanten + 2.

Eulers Formel für Polyeder scheint keinen Zusammenhang mit dem Satz von Pick zu haben: Die Polyeder sind dreidimensional, die Polygone zweidimensional. Bei Pick liegen die Ecken auf einem Gitter, bei Euler kommt kein Gitter vor. Und doch folgt die Polyederformel verblüffend einfach aus dem Satz von Pick.

Ein letztes Beispiel: Wählen wir irgendeine natürliche Zahl, sagen wir 5. Die Folge von Farey F5 erhält alle Fünftel zwischen 0 und 1 und dazu noch alle Viertel, alle Drittel und alle Halben (Halbes gibt es nur eines, nämlich 1/2). Einige Brüche kommen mehrmals vor, da nimmt man den gekürzten: also nicht 2/4, sondern 1/2. Reihen wir diese Brüche der Größe nach und fügen wir als Endpunkte 0 und 1 dazu. Die schreiben wir auch als Brüche, also 0/1 und 1/1. Das ergibt also

F5=(0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1)

Der Hauptsatz für Farey-Folgen besagt: Nimmt man zwei aufeinanderfolgende Brüche, etwa 3/4 und 4/5, und multipliziert den Zähler des kleineren mit dem Nenner des größeren (also 3 mit 5), so ist das Produkt des Nenners des kleineren mit dem Zähler des größeren (also 4 mal 4) immer um 1 größer. Immer genau um 1. Das gilt nicht nur für F5, sondern auch für F23 und F276990 und überhaupt für alle Farey-Folgen.

Das ist ein kurioses Resultat, aber am kuriosesten daran ist: Es folgt unmittelbar aus dem Satz von Pick. Wie kann das sein? Bei Farey liegen Brüche zwischen 0 und 1 aufgefädelt wie Schwalben auf einem Telefondraht. Was hat das mit Gittern zu tun? Mit Polygonen? Mit Flächeninhalt? Es hat sogar sehr viel damit zu tun – und wieder hat der Beweistrick (der ganz einfach ist, wenn man ihn kennt) etwas Zauberhaftes an sich. Deswegen gilt der fabelhafte Satz von Pick als kleines mathematisches Juwel. Sein Beweis ist so einsichtig und schön, dass er fast heiter wirkt – was das tragische Ende seines Entdeckers noch trauriger macht.

Schade, dass der Satz von Pick im Schulstoff nicht vorkommt. Der Stundenrahmen ist so knapp, dass keine Zeit bleibt für die unterhaltsamen Aspekte der Mathematik. Dadurch entgeht den Kindern etwas, und auch den Erwachsenen. Vielen Menschen bereitet Denken Vergnügen. Sie genießen Sudokus und viele andere Spiele, die Scharfsinn verlangen. Und ahnen oft nicht, was die alten Griechen wussten: dass die Mathematik das Spiel der Götter ist. (Karl Sigmund, 14.3.2020)