Ein Möbiusband ist das vielleicht größte mathematische Kuriosum, das sich am einfachsten herstellen lässt: Man nehme einen Papierstreifen, verdrehe ihn um 180 Grad und klebe die beiden Enden zusammen, und fertig ist das Band, das nach dem deutschen Mathematiker und Astronomen August Ferdinand Möbius (1790–1868) benannt ist, der die topologischen Eigenschaften dieses Objekts 1858 erstmals im Detail beschrieb.

Die sind ziemlich faszinierend. Um nur die wichtigsten zu nennen: Das Möbiusband hat nur eine Fläche und auch nur einen Rand. Schneidet man mit einer Schere bei einem gewöhnlichen Papierring entlang seiner Mittellinie einmal um das ganze Band, erhält man zwei getrennte Ringe. Macht man das Gleiche mit einem Möbiusband, entsteht nur ein Ring, der doppelt verdreht ist.

Aus diesen und zahlreichen anderen Gründen haben Möbiusschleifen viele Mathematikerinnen, Künstler – Primus inter Pares M. C. Escher – und Wissenschafter in einer Vielzahl von Bereichen inspiriert.

Unklare Längenverhältnisse

Sie geben auch jede Menge Variationen und Probleme her. Grundsätzlich sind lange, dünne Möbiusbänder leichter herzustellen als breite kurze. Wenn man langsam an einem Ende einer nichtverklebten Möbiusschleife zieht, um diese zu verkürzen, entstehen letztlich drei miteinander verbundene Dreiecke. Man erhält auf diese Weise ein im Vergleich zur Breite extrem kurzes Möbiusband, das vom Mathematiker W. Wunderlich 1962 ausführlicher beschrieben wurde.

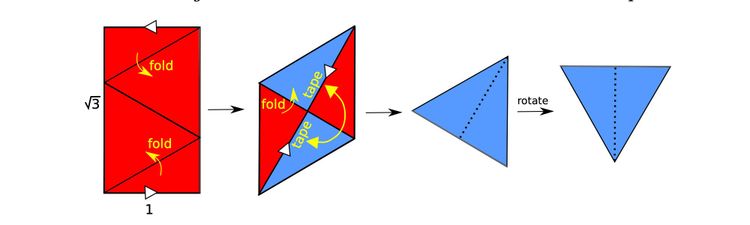
Bleibt die Frage, ob das tatsächlich das im Vergleich zur Breite kürzeste Ausgangsmaterial für ein Möbiusband ist. Und wenn ja, wie sich das in eine Formel und einen Beweis bringen lässt. 1977 stellten die Mathematiker B. Halpern und C. Weaver die Hypothese auf, dass die minimale Länge des dreieckigen Möbiusbands im Verhältnis zur Breite vermutlich √3 beträgt, also in etwa das 1,73-Fache. Konkret: Ist der Papierstreifen zehn Zentimeter breit, muss er mindestens 17,3 Zentimeter lang sein, damit er zu einem Möbiusband werden kann. (Wenn wir es ganz genau nehmen, ist das dreieckige Möbiusband der Grenzwert für Papier-Möbiusbänder, der für eine idealisierte mathematische Version von Papier gilt, das unendlich dünn, glatt und nicht dehnbar ist.)

Doch in den folgenden 46 Jahren war niemand in der Lage, diese Behauptung zu beweisen. Halpern und Weaver konnten in ihrem Aufsatz letztlich auch nur zeigen, dass das Verhältnis zwischen Länge und Breite eines Möbiusbandes größer als π/2, also etwa 1,57 sein muss.

Dieses ungelöste Rätsel hat irgendwann auch das Interesse des angesehenen US-Mathematikers Richard Evan Schwartz von der Brown University im US-Bundesstaat Rhode Island geweckt. Schwartz, der einige tolle Mathe-Kinderbücher verfasst, hat eine Vorliebe für einfache Probleme, die Mathematiker vor schwere Probleme stellen: "Ich mag es, wenn niemand eine Idee hat, was zu tun ist", sagt er im Gespräch mit "Sciencenews". Ein weiterer Vorteil solcher Probleme: "Wenn ich bei dieser Aufgabe versage, ist das keine Schande. Ich bin dann eben genau wie alle anderen."

Doch nicht die Wurzel aus 3?

Schwartz konzentrierte sich auf eine Schlüsseleigenschaft von Möbiusstreifen: Wenn sich das Papier in der aus Dreiecken bestehenden Möbiusschleife faltet, gibt es an jedem Punkt des Bandes eine Richtung, in der das Papier einer geraden Linie von Kante zu Kante folgt, ohne irgendeine Krümmung. Er erkannte, dass es in jedem Möbiusband immer zwei solche Linien geben muss, die senkrecht und in derselben Ebene liegen, wie beim Buchstaben T.

Anhand der Art und Weise, wie sich das Papier verformt, um diese T-Form zu bilden, fand Schwartz ein neues Mindestverhältnis zwischen Länge und Breite. Zu seiner Enttäuschung war es nicht √3, sondern eine Zahl, die etwas kleiner ist, etwas über 1,694, wie er 2021 im Fachblatt "Geometriae Dedicata" berichtete. Hier die dazugehörige Formel:

Schwartz wandte sich daraufhin anderen Themen zu, konnte aber nicht aufhören, über das Problem nachzudenken. Eines Tages begann er aus einer Laune heraus, mit Papierstreifen zu spielen. Und bald musste er feststellen, dass er einen fundamentalen Fehler gemacht hatte. Schwartz war davon ausgegangen, dass das Aufschneiden eines Möbiusstreifens entlang einer Diagonale und das Abflachen ein Parallelogramm ergeben. Doch als Schwartz einen seiner Papier-Möbiusstreifen aufschnitt, sah er kein Parallelogramm, sondern ein Trapez vor sich.

Einfacher Programmierfehler 

"Ich sagte sofort: 'Oh, oh'", so Schwartz im Rückblick auf sein Heureka-Erlebnis. Es war ein ziemlich trivialer Fehler, der dadurch entstanden war, dass sich der Mathematiker bis dahin nur am Computer mit dem Möbiusproblem beschäftigt hatte. Er vertat sich bei der Programmierung, was letztlich zum Parallelogramm-Fehler führte. "Als ich den Fehler einmal gemacht hatte, war es, als ob er sich in meinem Gehirn festgesetzt hätte." Dass ihm der Fehler nicht schon früher aufgefallen war und er erst so spät zum Papier griff, ist umso erstaunlicher, als eines von Schwartz’ Hobbys darin besteht, aus Papier kunstvolle Masken zu basteln.

Als er die Berechnung mit der Trapezkorrektur wiederholte, kam √3 heraus, wie er in seinem neuen Beweis schreibt, der bislang nur als Preprint auf Arxiv erschien und dort erst vor wenigen Tagen in seine aktuelle Fassung gebracht wurde. Damit dürfte nach 46 Jahren tatsächlich bewiesen sein, dass die Länge eines Möbiusbandes zumindest so groß sein muss wie das √3-Fache seiner Breite. (tasch, 13.10.2023)