Sir Roger Penrose hat nicht nur als Kosmologe und theoretischer Physiker Herausragendes geleistet. Der Nobelpreisträger des Jahres 2020, der diese Auszeichnung für seine Arbeiten über Schwarze Löcher erhielt, hat auch in Sachen Parkettmuster Geschichte geschrieben und sich unsterblich gemacht.
Ein Physiker und Mathematiker als genialer Bodenverleger?
Nein, aber fast: In den 1970er-Jahren legte Penrose – unter anderem angeregt von Johannes Kepler, Albrecht Dürer, aber auch neueren Diskussionen in den 1960er-Jahren – Arbeiten zu geometrischen Formen vor, die sogenannte aperiodische Muster ergeben, sich also nie wiederholen, ohne dabei Zwischenräume aufzuweisen. Diese Arbeiten wurden so einflussreich, dass diese geometrischen Formen heute als Penrose-Parkettierung bezeichnet werden. Und es gibt Böden, die nach den Designs von Penrose verlegt wurden.
Aperiodische Muster in der Natur
Diese Form aperiodischer Muster kommt – anders als der britische Physiker ursprünglich vermutete – auch in der Natur vor: 1982 entdeckte nämlich sein israelischer Kollege Daniel Shechtman sogenannte Quasikristalle, in denen die Atome beziehungsweise Moleküle ebenfalls in einer geordneten, aber aperiodischen Struktur angeordnet sind. Shechtman wurde dafür lange und heftig (unter anderem als "Quasiwissenschafter") kritisiert. 2011 wurde ihm für seine Entdeckung der Chemienobelpreis zugesprochen. Und mittlerweile gibt es sogar schon Anwendungen für diese Quasikristalle.
Doch zurück zu Penrose. Vor dessen Arbeiten versuchten Mathematikerinnen und Mathematiker in den 1960er-Jahren, die Zahl der Kacheln zu minimieren, die solche aperiodischen Muster ohne alle Lücken ergeben. Bis Penrose sich damit zu befassen begann, war die Minimalzahl noch sechs; Penrose konnte diese Zahl auf vier Grundelemente reduzieren:
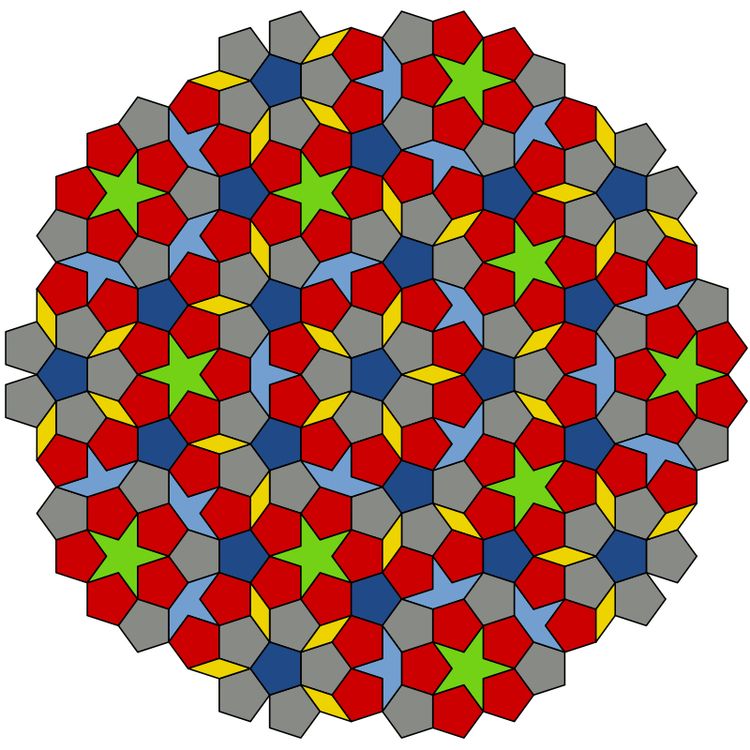
Durch weiteres Zerlegen in Einzelteile gelang dem mittlerweile 91-jährigen Briten der Beweis, dass bereits zwei verschiedene Kachelformen, gemeinsam und richtig verlegt, ebenfalls das Tor zur Unendlichkeit aufstoßen können:

Mittlerweile gibt es Dutzende solcher aus zumindest zwei Elementen zusammengesetzten Formen, die für aperiodische Muster sorgen. Doch seit Penrose seine Pionierarbeiten verfasste – die erste davon vor genau einem halben Jahrhundert –, fragen sich Mathematikerinnen und Mathematiker, ob es womöglich auch eine einzelne Kachelform gibt, die für solche aperiodischen Muster sorgt, die sich bis in alle Unendlichkeit nicht wiederholen.
Im Englischen wird diese seit Jahrzehnten heftig gesuchte Form als "Einstein" bezeichnet, hergeleitet vom deutschen Ausdruck "ein Stein" (und nicht vom Begründer der Allgemeinen und der Speziellen Relativitätstheorie, aus deren Ableitung Penrose wiederum seine mit dem Nobelpreis gewürdigte mathematische Beschreibung der Schwarzen Löcher lieferte).
Durchbruch eines Hobbymathematikers
Eine solche Kachel dürfte nun tatsächlich entdeckt worden sein. Der ziemlich sensationelle Durchbruch gelang David Smith, einem britischen Hobbymathematiker, der sich selbst als "fantasievoller Tüftler von Formen" bezeichnet. Dieser erste je entdeckte "Einstein" ist zur Überraschung der Fachleute ziemlich einfach, nämlich nur 13-seitig, und sieht entfernt wie ein Hut aus, weshalb diese Form von ihrem Entdecker so genannt wird.
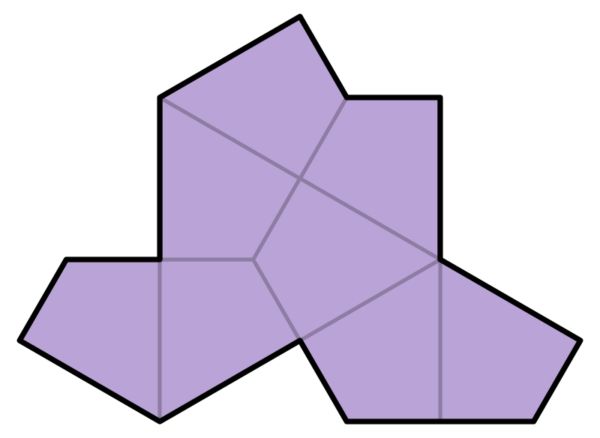
Zudem entdeckte der 64-jährige pensionierte Drucktechniker aus Bridlington in East Yorkshire auch noch eine zweite, etwas weniger komplexe Form, die er "Schildkröte" nennt – ebenfalls wegen der Ähnlichkeit mit dem Reptil. In seinem Blog gibt es eine Art "Skizzenbuch", das nachvollziehen lässt, wie der Hobbymathematiker auf die beiden Formen stieß, von denen der Hut mittlerweile auch mathematisch genau analysiert wurde.
Zwei Beweise auf 89 Seiten
Seit knapp einer Woche sind dessen einzigartige Eigenschaften nicht nur in einem auf der Preprint-Plattform Arxiv.org veröffentlichten Artikel beschrieben. Auf 89 Seiten tritt Smith mit Unterstützung dreier Profis aus der Mathematik und der Informatik auch den Beweis an, warum der Hut tatsächlich aperiodische Muster liefert und ein Einstein ist. (Wobei die Beweisführung ausschließlich Sache der drei Co-Autoren und er dabei keine große Hilfe war, wie Smith in der "New York Times" einräumt.)

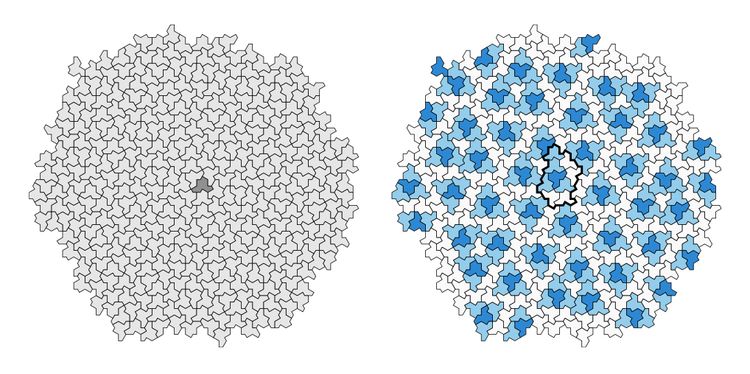
Zum einen behauptet das Team, dass sich diese Kacheln in größeren Clustern anordnen, den sogenannten Metakacheln. Diese Metakacheln wiederum formieren sich dann in noch größeren Superkacheln, und immer so weiter. Das ist eine Art hierarchischer Struktur, die für nichtperiodische Kacheln üblich ist. Auf diese Art lässt sich zeigen, dass die 13-seitigen Hüte eine unendliche Fläche ausfüllen könnten, ohne dass sich die Muster je wiederholen.
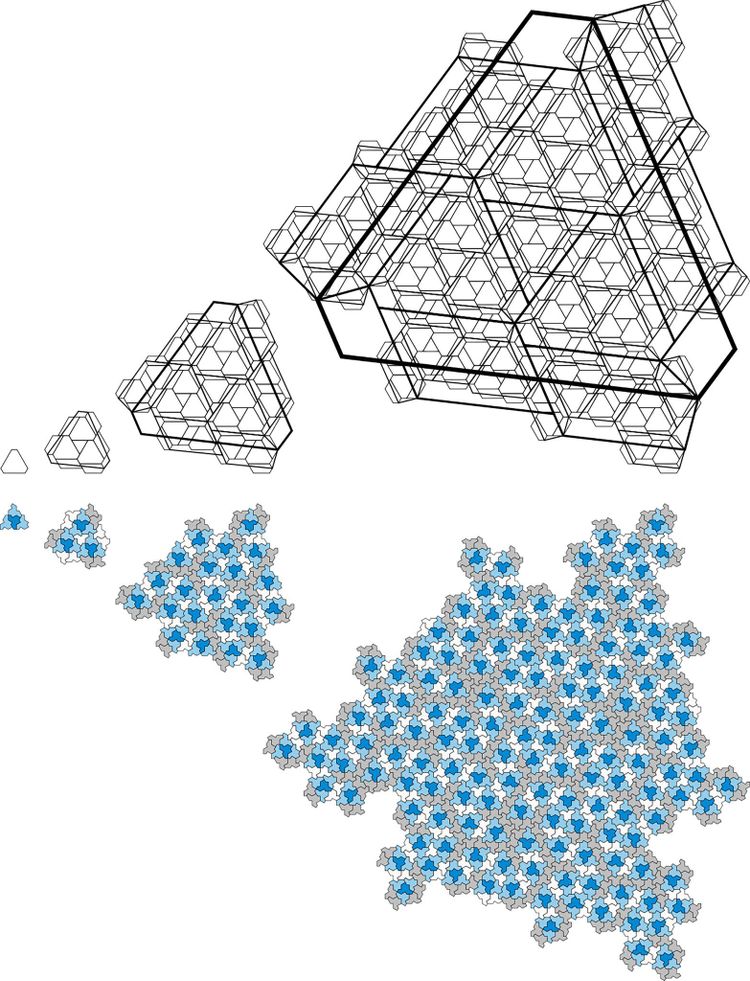
Der zweite Beweis beruhte auf der Tatsache, dass der Hut Teil eines Kontinuums von Formen ist: Indem Smith mit seinen Kollegen die relativen Längen der Seiten der Form schrittweise veränderte, konnten sie eine Familie von Kacheln bilden, die das gleiche sich nicht wiederholende Muster annehmen können.
Durch die Betrachtung der relativen Größen und Formen der Kacheln an den Extremen dieser Familie – die eine hat die Form eines Chevrons (das ist das sägezahnartige Muster der Austrittskante eines Triebwerks), die andere erinnert an einen Kometen – konnte das Team ebenfalls zeigen, dass der Hut nicht in einem periodischen Muster angeordnet werden kann.
Offiziell ist die Entdeckung zwar noch nicht bestätigt, da der Artikel noch nicht begutachtet und noch in keinem Fachjournal publiziert wurde. Doch alle befragten Experten sind sich ziemlich einig, dass der Hut tatsächlich der erste je entdeckte Einstein ist. Wer also zu Hause das Badezimmer auf sehr originelle Weise verfliesen will oder nach einem wirklich einzigartigen Parkettbodenmuster sucht, für den gibt es ab sofort wohl nur ein einziges Modell. (Klaus Taschwer, 26.3.2023)